题 目：基于累积协方差矩阵的多元响应变量的充分降维方法

主讲人：周亭攸副教授

时  间：2023年4月20日（周四）14:30-15:30

地  点：6号学院楼500会议室

主办单位：2138cn太阳集团古天乐 浙江省2011“数据科学与大数据分析协同创新中心”

摘 要：

度量和检验两个随机变量之间的相互依赖关系历来都是进行统计研究之中的一个基本问题。本文提出了一种新的稳健度量——累积协方差矩阵(Cumulative Covariance Matrix， 简称CCM) ——用来检验一个p维随机向量x的条件均值是否依赖于另一个q维随机向量y。我们首先证明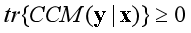恒成立，并且，当且仅当y的条件均值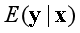不依赖于x时，等号成立。随后研究其样本估计量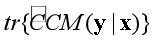的渐近性质并证明：当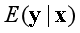不依赖于x时，此样本估计量是 n相合的; 否则则是根号n相合的。此外，还通过大量的数值模拟说明，基于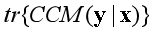的条件均值独立性检验具有良好的大小和功效，并且该优势在数据中存在极端值时更加显著。最后，我们基于累积协方差矩阵提出了一种针对多元响应变量的充分降维方法，用来估计中心降维子空间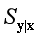，并证明了该方法的相合性。该降维方法不用考虑切片，能够避免多重随机投影而导致的降维结果的不稳定，并且在响应变量中存在异常值时具有稳健的性质。最后通过广泛的数值模拟和人体血压的实际数据分析展示了该降维方法的有限样本性质。

主讲人简介：

周亭攸，女，1990年生，2017年毕业于上海财经大学统计与管理学院，博士学位。现任职于2138cn太阳集团古天乐，副教授。长期从事统计学理论和方法研究，研究方向集中在高维及超高维数据统计分析、半参数回归模型统计推断等领域。

欢迎各位老师和同学积极参加！